찬

백엔드 엔지니어에서 AI 엔지니어로 항해 중이에요☺️

Numpy - 기본

5 minute read

1. Vector Operations

import numpy as np

# 파이썬 일반적인 더하기 연산
u = [1, 2, 3]
v = [4, 5, 6]
print(f"plus list = {u + v}")

# 벡터 덧셈 구현
plus1 = [
    u_val + v_val 
    for (u_val, v_val) in list(zip(u, v))
]
print(f"plus vector = {plus1}")

# Numpy를 이용한 벡터 덧셈 (Numpy의 연산자 오버로딩)
plus_np = np.array(u) + np.array(v)
print(f"plus vector (np) = {plus_np}")

plus list = [1, 2, 3, 4, 5, 6]
plus vector = [5, 7, 9]
plus vector (np) = [5 7 9]

2. Tensor

import numpy as np

empty_tensor = np.array([[[],[]],[[],[]]])
print(f"tensor shape: {empty_tensor.shape}")
print(f"tensor size: {empty_tensor.size}") # 2 x 2 x 0

tensor = np.array([[[1],[2]],[[3],[4]]])
print(f"tensor shape: {tensor.shape}")
print(f"tensor size: {tensor.size}") # 2 x 2 x 1


tensor shape: (2, 2, 0)
tensor size: 0
tensor shape: (2, 2, 1)
tensor size: 4

1) reshape

import numpy as np
tensor = np.array([[[1],[2]],[[3],[4]]])
print(f"shape = {tensor.shape}")
print(
    "reshape:\n",
    np.reshape(tensor, (1, 2, 2))
)
print(
    "reshape:\n",
    np.reshape(tensor, (1, 2, -1))
)

shape = (2, 2, 1)
reshape:
 [[[1 2]
  [3 4]]]
reshape:
 [[[1 2]
  [3 4]]]

3. Function

1) zeros

import numpy as np

print(
    np.zeros((4, 3, 2))
)

[[[0. 0.]
  [0. 0.]
  [0. 0.]]

 [[0. 0.]
  [0. 0.]
  [0. 0.]]

 [[0. 0.]
  [0. 0.]
  [0. 0.]]

 [[0. 0.]
  [0. 0.]
  [0. 0.]]]

2) ones

import numpy as np

print(
    np.ones((4, 3, 2))
)

[[[1. 1.]
  [1. 1.]
  [1. 1.]]

 [[1. 1.]
  [1. 1.]
  [1. 1.]]

 [[1. 1.]
  [1. 1.]
  [1. 1.]]

 [[1. 1.]
  [1. 1.]
  [1. 1.]]]

3) full

import numpy as np

print(
    np.full((4, 3, 2), fill_value=40)
)

[[[40 40]
  [40 40]
  [40 40]]

 [[40 40]
  [40 40]
  [40 40]]

 [[40 40]
  [40 40]
  [40 40]]

 [[40 40]
  [40 40]
  [40 40]]]

4) range

import numpy as np

print(
    np.arange(15)
)
print(
    np.arange(15, 20)
)
print(
    np.arange(15, 20, 2)
)

[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14]
[15 16 17 18 19]
[15 17 19]

5) linspace

import numpy as np

print(
    np.linspace(0, 10, 3) # 시작, 끝 값 포함
)

[ 0.  5. 10.]

6) normal

  • 정규분포에서 데이터를 추출
import numpy as np

print(
    "(1):\n",
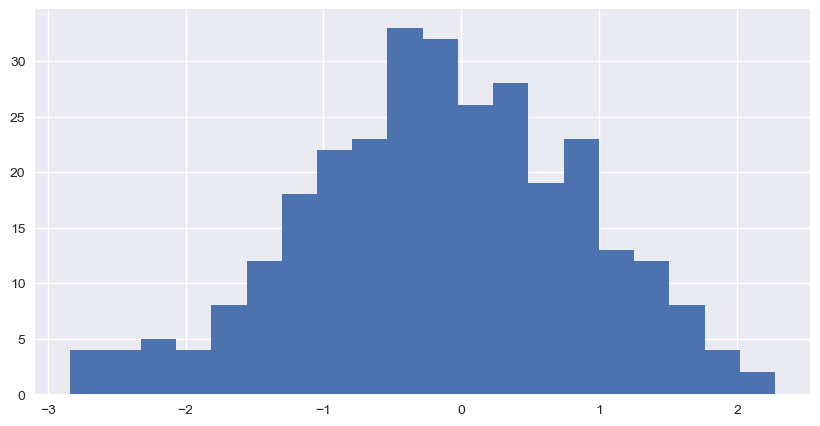
    np.random.normal(
        loc=0, # 평균
        scale=5, # 표준편차
        size=10 # 갯수
    )
)

print(
    "(4, 2):\n",
    np.random.normal(
        loc=[0, 1], # 평균 / Union[bool, int, float]
        scale=[1, 5], # 표준편차 / Union[bool, int, float]
        size=(4, 2) # 갯수 / _ShapeLike = Union[SupportsIndex, Sequence[SupportsIndex]]
    )
) # 

(1):
 [-1.95731126 -1.90675734  6.17352222 16.02351182  1.48539524 11.16237614
 -6.55725407  1.43203681  9.44325562  7.82157837]
(4, 2):
 [[ -0.54754113   0.26006383]
 [ -1.81259151 -11.64953749]
 [ -0.70481288  -2.02977314]
 [ -1.12333622  -7.81040641]]

7) randn

  • 표준정규분포에서 값을 추출
import numpy as np
import matplotlib.pyplot as plt

plt.style.use("seaborn")

fig, ax = plt.subplots(figsize=(10, 5))

random_values = np.random.randn(300)
ax.hist(random_values, bins=20)
plt.show()

png

8) rand

  • 전 구간 값의 추출 확률이 동일 (from Uniform Distribution)
import numpy as np
import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(10, 5))

uniform = np.random.rand(5)
ax.hist(uniform)

png

9) uniform

  • 지정한 범위 내에서 동일한 확률로 값을 추출 (from Uniform Distribution)
import numpy as np
import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(10, 5))

ax.hist(
    np.random.uniform(low=-5, high=5, size=3)
)

png

10) randint

  • 지정한 범위 내에서 동일한 확률로 값을 추출 (from Uniform Distribution)
import numpy as np

print(
    np.random.randint(low=-5, high=5, size=3)
)

[-3 -5 -1]

11) flatten

  • vector 로 평탄화
import numpy as np

print(
    np
        .arange(16)
        .reshape(2, 4, 2)
        .flatten()
)

print(
    list(
        np
            .arange(16)
            .reshape(2, 4, 2)
            .flat
    )
)

[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]

4. Operator Overriding

  • Numpy 는 ndarray 의 연산자 오버로딩이 구현되어 있다.

1) vector - vector

import numpy as np 
a = np.random.randint(1, 5, (5, )) 
b = np.random.randint(1, 5, (5, )) 
print("a: ", a) 
print("b: ", b, "\n")
print("a + b: ", a.__add__(b)) 
print("a - b: ", a.__sub__(b)) 
print("a * b: ", a.__mul__(b)) 
print("a / b: ", a.__truediv__(b)) 
print("a // b: ", a.__floordiv__(b)) 
print("a % b: ", a.__mod__(b)) 
print("a ** b: ", a.__pow__(b))

a:  [1 1 2 1 1]
b:  [3 3 3 3 3] 

a + b:  [4 4 5 4 4]
a - b:  [-2 -2 -1 -2 -2]
a * b:  [3 3 6 3 3]
a / b:  [0.33333333 0.33333333 0.66666667 0.33333333 0.33333333]
a // b:  [0 0 0 0 0]
a % b:  [1 1 2 1 1]
a ** b:  [1 1 8 1 1]

2) matrix - matrix

import numpy as np 
M = np.random.randint(1, 5, (2, 3)) 
N = np.random.randint(1, 5, (2, 3)) 
print("M: \n", M) 
print("N: \n", N, '\n')
print("M + N: \n", M + N) 
print("M - N: \n", M - N) 
print("M > N: \n", M > N) 
print("M >= N: \n", M >= N)

M: 
 [[3 2 3]
 [3 2 2]]
N: 
 [[2 1 1]
 [2 3 2]] 

M + N: 
 [[5 3 4]
 [5 5 4]]
M - N: 
 [[ 1  1  2]
 [ 1 -1  0]]
M > N: 
 [[ True  True  True]
 [ True False False]]
M >= N: 
 [[ True  True  True]
 [ True False  True]]

5. Broadcasting

  • tensor의 차원, 원소의 갯수가 달라도 shape 에 매핑한 연산을 해주는 동작이다
  • shape의 매핑이 불가능한 경우에는 broadcasting 도 불가능하다.

1) 같은 차원의 tensor

from imagehash import NDArray
import numpy as np

A = np.arange(9).reshape(3, 3)
print(A.shape)
B = 10 * np.arange(3).reshape(-1, 3)
print(B.shape)
C = A + B
print(C)

(3, 3)
(1, 3)
[[ 0 11 22]
 [ 3 14 25]
 [ 6 17 28]]

import numpy as np

shape = (2, 3, 3)
tensor1 = np.random.normal(loc=0, scale=5, size=shape)
tensor2 = np.linspace(start=0, stop=5, num=9).reshape(1, 3, 3)
print(tensor1 + tensor2)

[[[ 9.12953843  1.47175842 12.00193402]
  [ 6.64098985 -4.40916224  5.29706066]
  [ 0.95522031  4.3088853   5.61501793]]

 [[-1.28809693  5.12414976  0.70989106]
  [ 3.16516936 -2.63488555 -4.27342152]
  [ 4.68412939 -2.31744839  7.01588788]]]

2) 다른 차원의 tensor

import numpy as np

tensor_3d = np.zeros(shape=(2, 3, 4))
tensor_2d = np.ones(shape=(3,1))
print(f"tensor_3:\n{tensor_3d}")
print(f"tensor_2:\n{tensor_2d}")
print(f"sum:\n{tensor_3d + tensor_2d}")

tensor_3:
[[[0. 0. 0. 0.]
  [0. 0. 0. 0.]
  [0. 0. 0. 0.]]

 [[0. 0. 0. 0.]
  [0. 0. 0. 0.]
  [0. 0. 0. 0.]]]
tensor_2:
[[1.]
 [1.]
 [1.]]
sum:
[[[1. 1. 1. 1.]
  [1. 1. 1. 1.]
  [1. 1. 1. 1.]]

 [[1. 1. 1. 1.]
  [1. 1. 1. 1.]
  [1. 1. 1. 1.]]]

6. Indexing and Slicing

  • tensor에 index를 통해 접근할 수 있다
import numpy as np

tensor_3d = np.arange(27).reshape(3, 3, 3)
print(f"tensor_3d:\n{tensor_3d}")

print(f"tensor_3d[0][0][0]: {tensor_3d[0][0][0]}")
print(f"tensor_3d[:2][0]: {tensor_3d[:2][0]}")
print(f"tensor_3d[:2][0][:2]: {tensor_3d[:2][0][:2]}")

tensor_3d:
[[[ 0  1  2]
  [ 3  4  5]
  [ 6  7  8]]

 [[ 9 10 11]
  [12 13 14]
  [15 16 17]]

 [[18 19 20]
  [21 22 23]
  [24 25 26]]]
tensor_3d[0][0][0]: 0
tensor_3d[:2][0]: [[0 1 2]
 [3 4 5]
 [6 7 8]]
tensor_3d[:2][0][:2]: [[0 1 2]
 [3 4 5]]

Comments

You May Also Enjoy